Double-precision Floating-point
This article looks at floating-point numbers. In particular, we concentrate on double-precision
floating-point.
Review of Integers
The natural integers 1, 2, 3, … are called natural because they are used to count
objects; for example, there were seven stars in the consternation Ursa Major (Big
Dipper, or Plough) long before humans came along to count them.
Computers store information in binary form by using two-state devices (typically,
on or off) to represent information. We employ the natural binary-weighted positional
system to represent data so that the binary string 011010 is equivalent to 0 x 25
+ 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 = 0 + 16 + 8 + 0 + 2 + 0 = 26.
Computers with 8-bit data words can represent unsigned integers in the range 0 to
255. Sixteen bit integers can be represented in the range 0 to 65,535, and 32-bit
integers can be represented in the range 0 to 4,294,967,295.
We can extend the range of integers into the negative region. Since we can’t increase
the total number of integers represented by m bits (i.e., 2m unique values), we typically
use two’s complement notation to represent the signed range -2m-1 to 2m-1- 1 which
is 2m-1 negative values, zero, 2m-1-1 positive values giving 2m values in total).
Unfortunately, integers can’t be used to represent fractional values like ½ or
or √2. Such numbers are called real numbers and these have a fractional part (i.e.,
a part less than 1). Moreover, these numbers may be incapable of representation with
a finite number of digits using positional notation (for example, you can’t represent
⅓ exactly as a decimal fraction – you can write 0.333 or 0.333333333333333333, but
you can never exactly express ⅓). This inability to represent all real numbers exactly
in decimal or binary form has implications for the accuracy of calculations. In particular,
it has implications for the accuracy of chained calculation involving sequences of
arithmetic operations. Ultimately, this property of numbers can mean that the results
of some calculations are effectively meaningless. The computer scientist has to appreciate
this fact.
As well as representing fractional or real values, we have to represent a range of
values from the very large to the very small. Consider big numbers. The population
of the Earth is about 7,200,000,000 which is a moderately large number. If you want
a truly big number, then we can use the mass of the sun which is about 198,892,000,000,000,000,000,000,000,000
kg. In conventional arithmetic, we represent such large numbers by means of scientific
notation where we separate out precision and magnitude by writing numbers of the
form m x 10e, where m is a mantissa and e an exponent. In this case, the sun’s weight
can be written 1.98892 x 1030 kg. This notation requires fewer digits than integer
notation, but also provides fewer significant digits; for example, the weight is
represented by 1.98892 with provides a precision of one in 106.
As well as small numbers, we have to deal with tiny numbers; for example, the chance
of a US citizen being hit by lightning in any given year is about 1 in 500,000 or
0.000,005 or 5.0 x 10-6. The mass of an electron is 9.109,382,914 x 10-31 kg. This
notation uses a negative exponent to indicate tiny values.
So, we use scientific notation to represent large and small numbers by writing a
number in the form m x 10e. Typically, the mantissa is expressed in the range 1.000…000
to 9.999…999 when using scientific notation.
Floating-point
It was natural that our scientific notation would be converted into an appropriate
binary form for use by computers. This form is called binary floating-point. The
term indicates that the binary point is not at a fixed place in the number; its position
is variable. Although dealing with binary integers is easy because you have just
two choices: the length of the integer in bits and whether to used signed or unsigned
representation, dealing with floating-point is not. Most definitely not.
If you choose a floating-point representation of real numbers, you have at least
four factors to consider. The first is the way in which you represent positive and
negative numbers. The second choice is the number of bits dedicated to the mantissa
(this determines the precision of the number). The third choice is the way in which
the sign of the exponent is represented (e.g., 2+8 or 2-4). The fourth choice is
the number of bits for the exponent. If the exponent too short (too few bits), we
can’t handle very large and small numbers. If the exponent is needlessly large, we
waste bits that could be better used by the mantissa.
The actual situation (i.e., trade-offs in the design of floating-point numbers) is
even worse because there are additional considerations (such as guard bits and sticky
bits) that we can introduce later.
For a long time each computer manufacturer implemented their own floating-point standard;
each manufacturer choosing a different range/precision/accuracy trade-off. This situation
did not support portability in the industry and made academic research difficult,
because comparing results performed on different computers was not easy. However,
here we are talking about calculations at the cutting edge in astronomy or the numerical
simulation of airflow over an aircraft wing. The various floating-point standards
were better behaved when performing more mundane tasks (i.e., no long chains of calculations
and not relying on all the avaialbe precision).
A great step forward took place in the 1980s when the IEEE produced a standard for
the floating-point representation of real numbers. The full name of the standard
is IEEE 754-1985 Standard for Binary Floating-point Arithmetic. This standard comprised,
in fact, a family of standards for floating-point numbers represented as 32 bit,
64 bits, and 128 bits. In this article we will look at the standards for 64-bit floating-point
numbers (also called double precision).
IEEE 754 defines:
- Storage formats
- Precise specifications of how results are generated
- The handling of special (non-floating-point values)
- The handling of exceptions and illegal operations
Double Precision IEEE 754 Format
The IEEE double-precision floating-point format uses a 64-bit word and is called
double in C and REAL*8 in FORTRAN.
Floating-point numbers are stored in normalized form to make greatest use of the
available precision; that is, the mantissa is always in the range 1.000…00 to 1.111…11.
To illustrate this notion consider a 5-bit mantissa with the normalized value 1.1101.
If this number were deformalized to 0.0111, we would have lost two bits of precision.
A normalized number always has a leading 1. If it always has a leading 1, we know
it’s there and do not have to store it. Consequently, when dealing with IEEE single-
and double-precision floating point numbers, we do not store the leading 1 in front
of the mantissa. This technique saves a single bit of storage. The actual number
stored in the mantissa field of an IEEE 754 floating-point numberis the fractional
mantissa field F. When the floating-point number is read from memory (unpacked),
the leading 1 is re-inserted. In other words, the normalized mantissa is 1.F but
we store only the F.
The format of a double-precision value is:
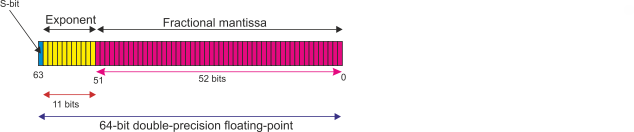
The sign-bit, S, is the most-significant bit, bit 63, and is 1 to represent a negative
number and 0 to represent a positive number. This mechanism is, of course, the same
as sign and magnitude notation.
The exponent occupies 11 bits from bit 52 to 62. In principle, this gives an exponent
range of 0 to 211 - 1 = 0 to 2047. In practice, this is not the actual exponent range
for two reasons: first, biased representation is used and second, certain exponents
are reserved as special tokens.
Negative exponents are handed by adding a constant to all actual exponents. This
constant is 1023 (i.e., 210 - 1). Suppose the actual exponent is 1. We add the bias
of 1023 and store 1024. When we read the biased exponent we subtract the 1023 bias
to get 1024 - 1023 = 1.
Suppose that the actual exponent is -6, a negative value. Adding the 1023 bias to
-6 gives 1017; that is, we have avoided having a negative value of the exponent.
If the actual exponent is -1000, we add the bias 1023 to get -1000 + 1023 = 23.
We cannot have a true exponent of -1023 because that would require a stored exponent
of -1023 + 1023 = 0 and that exponent value is forbidden. The reason for this is
practical. The stored exponent 0 is reserved for special applications as we shall
soon see.
The smallest stored exponent Emin is 1 corresponding to an actual exponent of 21-1023
= 2-1022.
The largest stored exponent is Emax is 2046 corresponding to an actual exponent of
22046-1023=21023.
The all zeros exponent, 00000000000, does not represent 20-1023 = 2-1023. It represents
a signed zero if the mantissa is 0. Let’s say this once again: if the mantissa and
the exponent are both all zeros then the floating-point number is 0. This arrangement
makes it easy to test for the value 0.
Using a biased exponent representation for floating-point numbers means that they
are lexically ordered. Lexical ordering (or lexicographical ordering) means dictionary
order; that is, in the same order that they would be stored as words in a dictionary.
In the case of floating point numbers it means that their order in terms of size
is the same order they would have if they were interpreted as integers. Consequently,
you can compare two floating point numbers using a simple integer comparator without
having to worry about exponent or mantissa. That’s nice.
However, there are exceptions to the lexical ordering. First, the ordering excludes
the sign-bit. Second positive and negative zero are special cases. Third, the NaN
(not a number) is not included.
If the mantissa is not zero (but the exponent is) then the value is a subnormal;
that is, a number too small to be represented precisely in IEEE 754 double-precision
format.
The other special exponent is all 1s, 11111111111. If the mantissa is not zero, this
represents a NaN or not-a-number. A NaN is a value outside the floating-point system
and is programmer defined. In other words, a NaN allows programmers to manipulate
non-floating-point values.
If the exponent is all 1s and the mantissa is 0, then the number is treated as infinity.
The 52-bit fractional mantissa is stored in bits 0 to 51; for example if the true
mantissa were 1.125 (1.001 in binary) the fractional mantissa would be stored as
00100000000000000000000000000000000000000000000000. As you can see, the leading 1
has been dropped.
Example
Consider the decimal value -42.625
The sign is negative so that S = 1.
42.625 can be converted to binary form as 101010.101
We can normalize this to 1.01010101 x 25.
The exponent is 5. In biased form this is 5 + 1023 = 1028 = 10000000011
The mantissa is 1.01010101 or 01010101 in fractional form.
We can now write the double-precision IEEE floating-point version of -42.625 as
1 10000000011 0101010100000000000000000000000000000000000000000000
In hexadecimal form, this is C035500000000000.
Range
The largest normalized value we can represent in 64-bit double-precision format is
1.1111111111111111111111111111111111111111111111111111 x 22046-1023 = 1.111…111 x
21023
This is approximately equivalent to the decimal value 1.8 x 10308. It is impossible
to specify a value greater than this. If you try to, you generate an exponent overflow
(an exponent bigger than the maximum in 11 bits) and the resulting value is stored
as the special number infinity.
The minimum normalized number is 2.2 x 10-308. The corresponding decimal precision
is approximately 15 digits.
This range of values can cope with the astronomical values we mentioned at the beginning
of this section. However, 15 places of decimal precision are not always sufficient
for some scientific calculations or for applications where two nearly identical numbers
are subtracted leading to a catastrophic loss of precision.
Floating-point Characteristics
Floating-point numbers are not exactly like real-numbers for several reasons. Floating
point numbers suffer from a floating-point error caused by approximating a real number
to a floating-point number using a finite number of bits.
When a real number is approximated, the new value can be rounded to a finite number
of bits in several ways; for example, simple truncation, rounding up or rounding
down, rounding towards zero, and so on.
Floating-point numbers form a finite and discrete set. If you are using 64 bits to
represent real values, then there can be only 264 different possible values. Floating-point
numbers are not evenly distributed; that is the interval between consecutive floating-point
numbers varies with the size (magnitude) of the number.
A key parameter of a floating-point system is called machine epsilon, machine. It
is defined as the smallest number such that 1 + machine > 1. The value of machine
epsilon is determined by the size of the least-significant bit of the mantissa. In
the case of double-precision arithmetic, machine = 2-53 (i.e., approximately 2.2
x 10-16).
In double-precision floating-point arithmetic, the smallest subnormal number is 2-1074
which is approximately 4.9 x 10-324. There is only one number smaller than this,
and that is zero. The smallest subnormal is the smallest mantissa with the smallest
exponent which is
0.000000000000000000000000000000000000000000000000001 x 2-1022 = 2-52 x 2-1022 =
2-1074.
This value is, of course machine epsilon multiplied by the most negative exponent;
that is, machine x 2Emin
Note that the range of double-precision floating-point values quoted by high-level
language manuals is 4.94065645841246544 x 10-324 to 1.79769313486231570 x 10308.
This range covers the smallest representable number to the largest number prior to
exponent overflow.
Demonstration of Floating-point Distribution
If would be nice to plot each of the 264 discrete double-precision on a graph but
that would take a rather large sheet of paper. Let’s take a tiny system for demonstration
and assume that we have a floating point number represented by a 2-bit mantissa and
a 2-bit exponent (we’ll assume positive numbers only, actual mantissas rather than
fractional mantissas, and exponents biased by 2. We’ll forget about NaNs and special
exponents but will regard a 0 exponent as representing zero).
A four-bit floating point number provides valid exponents of
Binary value Exponent Multiplier
00 special special
01 -1 x 0.5
10 0 x 1.0
11 1 x 2.0
For example, if the binary value of the exponent is 11, the actual exponent is 3
- 2 = 1 and the mantissa is multiplied by 21 = 2.
The mantissas are
Binary value Mantissa
00 0.0 (zero)
01 0.5 (unnormalized)
10 1.0
11 1.5
Applying exponents to mantissas, the valid floating-point numbers are:
0, 0.25, 0.50, 0.75, 0, 0.50, 1.0, 1.5, 0, 1.0, 2.0, 3.0, 0, 2.0, 4.0, 6.0
The values in red represent unnormalized values (i.e., the leading bit is 0 rather
than 1). The following table defines all possible values of the 4-bit code.
Code Value Notes
0000 0 zero exponent is 0
0001 0 zero exponent is 0
0010 0 zero exponent is 0
0011 0 zero exponent is 0
0100 0 unnormalized zero mantissa
0101 0.25 unnormalized
0110 0.50
0111 1.00
1000 0 unnormalized zero mantissa
1001 0.50 unnormalized
1010 1.00
1011 1.50
1100 0 unnormalized zero mantissa
1101 1.00 unnormalized
1110 2.00
1111 3.00
Note that the interval between consecutive values is not constant and depends on
the exponent (because the minimum step is multiplied by the exponent). Note also
that some values are not unique; for example 0.50 can be represented by 1.0 x 2-1
or by 0.5 x 20. However, the 0.5 x 20 value is unnormalized and has only one bit
of precision.
The value 0.25 is the smallest non-zero number that can be represented by this machine
and is therefore the machine epsilon.
The following figure shows all the positive floating point values that can be represented
by this system as blue dots. The 0.25 is in red to indicate that it is not normalized
because it is between zero and the smallest normalized number.

This figure illustrates zero, the smallest number, the maximum number and demonstrates
that the interval between consecutive numbers is not constant.
Further Comments
The mantissa of a floating-point number can be extended by the addition of one or
more guard bits in order to preserve accuracy during rounding. Guard bits are not
stored as part of a floating-point number; they are used during internal operations.
In other words, a floating-point number can be expanded internally in the ALU during
operations before being repacked for storage.
The greatest problems with floating-point arithmetic occur when two similar numbers
are subtracted or two widely differing numbers are added. Consider first subtraction.
We’ll use two normalised floating-point values with 6-bit mantissas: a = 1.00111
and b = 1.00110. If we subtract b from a, we get 1.00111 - 1.00110 = 0.00001. This
has only one bit of precision which may itself be wrong due to previous rounding.
Similarly, suppose we add 1.00111 x 25 to 1.11011 x 21. In order to add these numbers
we have to equalize exponents to get:
A = 1.00111 x 25
B = 0.00011011 x 25
The sum A+B is 1.01010011 when we truncate this mantissa to six bits we get 1.01010.
We have lost the contribution made by the three least-significant bits of B.

