Home Up

Home Teaching Glossary ARM Processors Supplements Prof issues About

Negative Numbers and Two’s Complement Arithmetic

We use negative numbers in everyday arithmetic to represent values that are less than zero; for example, we may speak of a -20° temperature or a growth rate of -1.25%. If we use negative numbers, so must our computers. This article looks at the nature of negative numbers and discusses how they are represented and manipulated in computers. In particular, we examine two’s complement arithmetic that is used to represent positive and negative binary integers.

We begin with a general introduction to numbers and then discuss ways of representing negative numbers. Next, we look at two’s complement numbers and show how they work, how they used, and how they are generated. The most important point of this article is to demonstrate that two’s complement arithmetic effectively abolishes subtraction by converting subtraction into the adding of a complement.

Historically, negative numbers are a relatively recent invention. You can pluck 5 apples off a tree. But what does -4 apples mean?  For a very long time, the notion of a negative value was an alien concept in most societies. The ancient Greeks dismissed negative numbers as nonsense. The Chinese introduced negative numbers about 2,000 years ago and, by the 7th century AD, negative numbers were being used in India to represent debits.

It wasn’t until the 17th Century that negative numbers gradually entered European mathematics. Indeed, negative numbers became respectable only after Leibniz introduced infinitesimal calculus.

Numbers

A number represents a means of counting objects or of measuring objects or quantities.  We can categorize numbers as follows:

Natural Numbers

The natural numbers are used to count objects; for example: 1, 2, 3, 4, 5. These numbers are positive integers ranging from 1 to infinity. Today, the value 0 is also considered as a natural number and, therefore, the set of natural numbers is 0, 1, 2, 3 4 …

Integers

Integers are whole numbers with no fractional part. The set of integers includes zero, natural numbers and negative natural numbers; that is …, -4, -3, -2, -1, 0, 1, 2, 3, 4, …

Rational Numbers

Rational numbers are those that can be represented as one integer divided by another (i.e., as fractions); for example, ½ or ¾ If a rational number is represented as m/n, then it is greater than 1 is m < n, and is less than 1 if m < n.

Irrational Numbers

An irrational number is one that cannot be represented in the form m/n where m and n are integers. The constant π is irrational and that be represented as 3.14 in three digits or 3.14159265358979 in 15 digits. However, even an infinite number of digits cannot represent π exactly. Similarly, √2 is an irrational number. Note that numbers like 1/3 are not irrational because they can be represented by a fraction (i.e., 1/3) even though that cannot be represented in real decimal form by a finite number of digits..

Transcendental Numbers

I suppose you could regard a transcendental number as a sort of überirrational number. A transcendental number is an irrational number that is not a root of a polynomial equation with rational coefficients. For example, the square root of 2 is irrational but it is not transcendental because it is a root of the equation x2 – 2 = 0. The two most well-known rational numbers are e and π.

Real Numbers

Real numbers are the numbers that we use in everyday scientific or financial calculations. A real number may be positive or negative and it is represented by an integer part and a fractional part; for example, 12.34567. This representation is called positional notation using the base 10 with a decimal point between the integer and fractional parts.

Real numbers include positive and negative integers, rational numbers and irrational numbers. You can think of a real number as being a point on a line that extends continuously from minus infinity to positive infinity.

Negative Integers

A traditional way of describing negative numbers is to refer to a scale or continuum of numbers with (typically) negative numbers on the left, zero in the middle and positive numbers on the right. See figure 1a. Such a diagram also demonstrates that adding x to number y means stepping x places to the right, and subtracting x from y means stepping x places to the left. If x is greater than y then we step past 0 into the negative region of the figure.

Figures 1(b) to 1(d) illustrate addition and subtraction as moving left or right along the scale of integers.

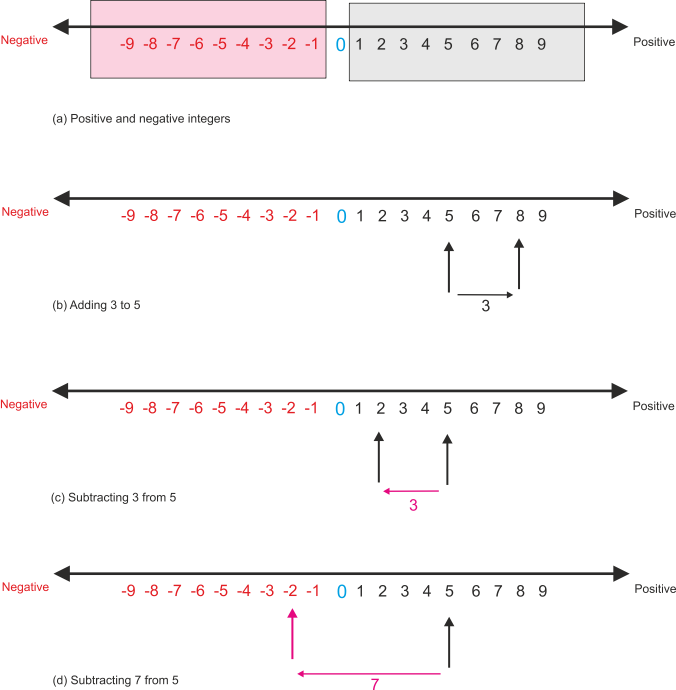
Figure 1 Illustrating positive and negative integers

Numbers and Computers

Computers represents signed an unsigned integers in exact binary integer form. The binary representation of an integer is exact and correct as long as there are sufficient bits to represent the number; for example, you can represent any integer in the range 0 to 255 in eight bits. If you want’ to represent 256 as an 8-bit integer – you can’t.

Real numbers are represented as floating-point numbers in the IEEE floating-point form -1S x 1.F x 2E+b, where S is a sign-bit, F is a fractional mantissa, E is the exponent, and b a bias. Irrational and transcendental numbers are all represented in real form by their appropriate approximations.

Representing Negative Numbers

How do we represent a negative number? We prefix it by a minus sign. The default sign is positive and we use a plus sign to make a positive number explicitly positive; for example -5, 6, +6. In my opinion, the purpose of the negative sign is not to create a negative number, but to tag a positive number to indicate that we have to treat it specially. Let me explain….

Consider -5. This is not really a negative number. It’s a positive number with a sign saying “subtract me”. Suppose we have the operation 9 + -5; that is 9 plus minus 5. Do we perform an addition as the expression calls for? No. We see the minus sign and perform a subtraction.  People automatically perform addition or subtraction depending on the sign of the number. Computers are rather different; there is no + or – sign.

How can we represent negative numbers in a computer? There are three general techniques. The first is called a biased representation and we actually remove negative numbers by representing the most negative number by 0. Consequently, which means all other numbers must be positive. For example, suppose we have numbers in the range -8 to +7. If we add 8 to all numbers, these numbers are represented by 0 to 15; for example, the value of -1 is 7, 0 becomes 8, and 2 becomes 10. All we have to do is to remember that our answer is too big by 8. This technique is used with floating-point exponents and we won’t go further into this topic here.

Another way of representing negative numbers is called sign and magnitude.  Here, we borrow a bit from a number and call it a sign bit; exactly the same way as we do in conventional arithmetic. By convention, a 0 bit is positive, and a 1bit is negative. In five bits 00010 is +2 and 10010 is -2. The sign and magnitude representation is used to represent the mantissa (fractional part) of floating-point numbers. It is not generally used to represent signed integer values. One often stated disadvantage of the sign and magnitude representation is that there are two values for zero. 000…00…000 is +0 and 100…00…00 is -0.

Finally, we come to the two’s complement representation of negative integers. Here, the negativeness of a number is indeed encoded into the number and it is a true negative. In other words, if you add a negative number you perform subtraction. In two’s complement arithmetic, adding 3 and 1 gives you 4. Adding 3 and (-1) gives you 2. Once more, in two’s complement arithmetic, you do not need to subtract negative numbers; you just add negative numbers. This is very attractive to the computer designer because it means computers don’t need subtraction circuits. An adder will perform both addition and subtraction.

Ten’s Complement Arithmetic

Before we look at two’s complement (computer) arithmetic, we really need to demonstrate that complementary arithmetic works in any base including the decimal base. A number N is represented in its negative form by bm - N, where b is the base and m the number of digits. Let’s use 4 decimal digits and let N be 25. In this case –N is represented by 104 – 25 = 10,000 – 25 = 9,975.

Suppose we want to calculate 73 – 25. Using subtraction we get 73 – 25 = 48.

Now consider adding the tens’s complement of 25 (i.e.,  9,975) to 73.

73 + 99,975 = 10,048.

As we are using 4-digit arithmetic, the result is actually 0048. This is the correct answer and we have performed subtraction by the addition of a complement.

Suppose we add 25 and 99,975. Here we are adding a number and its complement. We get 10,000 or 0000 in four digits. This is what we would get if we added 25 + (-25).

Note that the ten’s complement of a number is calculated by subtracting each of its digits from 9 (the nine’s complement) and then adding 1 to the final result. For example, in four digits the tens complement of 1234 is 9-1, 9-2, 9-3, 9-4 + 1 = 8765 + 1 = 8,766.

Consider 3,231 – 1,234. Adding the ten’s complement gives 3231 + 8766 = 11,997. In four digits this is 1,997 which is the correct value of 3,231 – 1,234 = 2,997.

Ten’s complement arithmetic was used by some mechanical adding machines prior to the age of the digital computer. Typically, each key or slot had two labels: the positive number and the nine’s complement value; for example, the key labelled 7 would also have the number 2 (nine’s complement) by it. To perform subtraction, you added the nine’s complement using the secondary number scale and then added 1 to the total.

Now let’s look at two’s complement arithmetic.

Two’s Complement Arithmetic

Above, we said that a number N is represented in its negative form by bm- N, where b is the base and m the number of digits. In binary arithmetic where b = 2, the two’s complement of N is defined as 2m – N.

Let’s begin with m = 4 (4-bit numbers), because that makes the arithmetic easy to follow. In unsigned integer arithmetic the range of values is from 0000 to 1111 (0 to 15 in decimal). Whatever we do, we cannot extend this range simply because there are only 16 possible combinations of four binary digits.

In four bits the representation of -0 is 24 – 0 = 10000 – 0000 = 10000 = 0000 in four bits. Thus, the representations of 0 and -0 are the same (which is reassuring). One advantage of two’s complement arithmetic is that there is only one value or representation of 0 and that value is 000 … 00 … 000 which means that testing for 0 in two’s complement arithmetic is the same as testing for 0 in unsigned arithmetic.

The representation of -1 is 24 – 1 = 10000 – 0001 = 1111

The representation of -8 is 24 – 8 = 10000 – 1000 = 1000

The following table shows how all 16 binary values are interpreted as a two’s complement value. Note that positive numbers are prefixed by 0 and negative numbers by 1. This means that the most-significant bit is a sign-bit and can be used to determine the sign of a number.

0000 = 0

0001 = 1

0010 = 2

0011 = 3

0100 = 4

0101 = 5

0110 = 6

0111 = 7

1000 = -8

1001 = -7

1010 = -6

1011 = -5

1100 = -4

1101 = -3

1110 = -2

1111 = -1

Note how the negative values or representations appear backwards; that is, the higher they look the smaller they are.

Consider the following examples of 4-bit twos complement arithmetic.

Example 1

Add 2 + 3.

0010 + 0011 = 0101

The result 0101 represents 5 which is the correct answer.

Example 2

Subtract 2 from 3 by adding the two’s complement representation of -2.

0011 + 1110 = 10001

The result in four bits is 0001 which is the correct answer

Example 3

Subtract 6 from 3 by adding the two’s complement representation of -6.

0011 + 1010 = 1101

The result is 1101. If we look at the table, this is interpreted as -3 which is the correct answer. Why don’t we interpret 1101 as 13? The answer is simple. If we are using unsigned integer arithmetic, we interpret the answer as an unsigned integer. If we are using signed two’s complement arithmetic, the answer must be treated as a two’s complement value.

Example 4

Subtract -2 from -5 by adding the two’s complement representation of -2 to the two’s complement representation of -5.

1011 + 1110 = 11001

The result is 11001. In four bits this is 1001.  If we look at the table, this is interpreted as -7 which is the correct answer.

Comment

Note that two’s complement arithmetic works for all combinations of a+b, a-b, -a+b, and -a-b. Note also that if a result is longer than four digits, we forget about the fifth digit. We will return to this point later. Now let’s look at two examples where the result goes out-of-range; that is, the result is not a valid two’s complement number in 4 bits.

Example 5

Add 2 + 7.

0010 + 0111 = 1001

The result 1001 represents -7 which is incorrect. This is because 2 + 7 = 9 which is larger than the largest positive value in four-bit two’s complement arithmetic. Of course, if we were using unsigned arithmetic, the result would have been correct because unsigned arithmetic in four bits allows a range 0 to 15.

Example 6

Subtract 5 from -6 by adding the two’s complement representation of 5 to -6.

1010 + 1011  =  10101

The result in four bits is 0101 which is +5 and is therefore the wrong answer.

Arithmetic Overflow

Examples 5 and 6 demonstrate that if we add together two positive values whose sum is greater than the maximum possible value we get an error. Similarly, if we add together two negative numbers whose value is more negative than the largest negative value, we also get an error.

In each of these cases the result, when interpreted as a two’s complement value, has an incorrect sign. This out-of-range effect is called arithmetic overflow.

It is impossible to get an out-of-range error when adding a valid negative value to a valid positive value because the result must be closer to zero than either of the numbers taking part in the addition.

How Does Two’s Complement Arithmetic Work?

Two’s complement arithmetic is not magic. Consider the representation of –p. This is defined as 2m – p. Now let’s subtract p from q; that is, we evaluate q – p.

To perform the subtraction, we add the two’s complement of p to get q + 2m – p = q - p + 2m

As you can see, we get the correct result q – p plus the  2m term. The value of 2m is the 1 in the m+1 bit position. This is the bit we discarded in the result.

Suppose we add together two negative numbers –p +  –q. In two’s complement arithmetic we perform the addition of the complements; that is,  2m – p+2m – q. If we rearrange the terms, we get 2m + (2m – p – q). This is the 2m term as before plus the two’s complement representation of –p – q which is the expected result.

Forming two’s Complement Numbers

We have pointed out that subtraction can be performed by adding the complement of a number. However, apart from defining the two’s complement representation of N as 2m – N, we haven’t said how we calculate this value. Since we use complementary arithmetic to avoid subtraction, it seems strange that we have to do a subtraction to generate the complement in the first place.

Let’s look at 2m – N.

We are using m bits to represent N. The value of N  which can be represented by the m digits {nm-1, nm-2, n1, n0} is therefore

N = nm-12m-1 + nm-22m-2  + nm-32m-3 + nm-42m-4   + n121 + n020    

In order for a number to be represented in its negative form, its most significant but, nm-1 must be 0.  Consequently, we can say that  N is:

N =  nm-22m-2  + nm-32m-3 + nm-42m-4  + n121 + n020    

We form the two’s complement of N by subtracting N from 2m. The value of 2m is 100 … 000, where there at m zeros following the leading 1. For example, in four bits 24 = 1000 and in 8 bits 28 = 100000000.

Now for the magic. Let’s rearrange 2m as 2m – 1 + 1. What does this look like? Well, 2m-1 = 111 … 111; that is, is a string of m – 1 ones. For example, 24 – 1 = 1111 and 28 – 1 = 11111111. Consequently, 2m can be rewritten as 111 … 111 + 1.

The final step is to write down the two’s complement representation of N at the bit level as:

111 … 111 + 1 – (nm-22m-2  + nm-32m-3 + nm-42m-4  + n121 + n020)

Rearranging the bits, we get:

1 - nm-22m-2 + 1 - nm-32m-3 + … + 1- n020 + 1

That is, the two’s complement of N is calculated by subtracting each bit of N from 1 and then adding 1 to the final total.

If ni = 1 then 1 – ni = 0 and if ni = 0 then 1 – ni = 0.

In other words, the two’s complement of N is calculated by inverting all the bits of N and adding 1.

Let’s test this. Consider N = 5 in 4 bits.

N = 0101.

24 – 0101 = 10000 – 0101= 1011

Inverting the bits and adding 1 gives: 1010 becomes 0101. Add 1 gives 1011.

These two results are the same. Consequently, the two’s complement of N can be calculated very rapidly in binary arithmetic by inverting the bits of N (simply by passing each bit of N through an inverting gate) and then adding 1 to the result.

In practice, the operation of A – B is performed by inverting the bits of B, adding those to the bits of A with the carry in to the first stage of the adder set to 1 to perform the adding of the additional 1.

Properties of Two’s Complement Numbers

The range of signed values that an  m-bit integer can represent  is -2m-1 to +2m-1 – 1. In 8-bit arithmetic, this is -128 to +127.

The two’s complement representation of zero is zero; that is, 000 … 00

The two’s complement is a true complement in the sense that –N + +N = 0

If a signed number in m bits is extended to m+1 bits, the most-significant bit (sign-bit) of the number is replicated. For example, in 4 bits -5 is represented by 1011. In 5 bits -5 is represented by 11011. It is for this reason that the assembly language level instruction arithmetic shift right operates by moving all bits one place right and replicating the sign bit.

Two’s Complement and Multiplication

Although two’s complement arithmetic works for addition and subtraction, it does not work for multiplication and division. Consider the product of P and –Q.

If we use two’s complement arithmetic, we get

P . (2m – Q) = 2mP – PQ.

What is the correct (expected answer)? When you multiply two m-bit values, the result is 2m bits long. Therefore the correct two’s complement representation of –PQ is 22m – PQ.

What we get using two’s complement arithmetic is 2mP – PQ .

To obtain the correct answer we would have to add the correction factor 22m  – 2mP  to the result. In practice, there are specific algorithms that can be used to multiply signed values; for example, Booths algorithm.

When using assembly language, some computer architectures provide different multiplication for signed and unsigned multiplication and division; for example, if you are using the 68K, the signed multiplication for registers D0 and D1 is expressed ad MULS D0,D1 and the unsigned multiplication of D0 and D1 is represented by MULU D0,D1.

Consequences of Two’s Complement Arithmetic

In four bits, which is the greater value 0011 or 0001. These values represents 3 and 2, respectively, in decimal and therefore 0011 > 0001.

Now consider 1011 and 1001. Which is the greater? In this case, the answer is not quite as simple. If we regard these are unsigned numbers, then 1011 > 1001 because 11 is greater than 9. However, if we regard these as signed numbers then 1001 > 1011 because -7 is greater than -3 (in terms of magnitude).

Instruction set designers provide the same compare instructions for both signed and unsigned quantities, but provide different conditional branch operations to allow you to branch on, say, greater than for signed and unsigned comparisons.

Examples

What are the three most common ways of representing signed numbers in computer arithmetic?

Sign and magnitude representation

Biased representation

Two’s complement representation

Why is two’s complement representation used to handle signed integers in binary arithmetic?

Because two’s complement numbers are easy to generate (invert the bits and add 1). In two’s complement arithmetic subtraction is performed by adding the complement of a number. Consequently, separate adders and subtractors are not needed. The most-significant bit of a two’s complement value is a sign-bit and is 1 to indicate negative and 0 to indicate positive or zero. Finally, a two’s complement number has only one value for zero which is 000 … 000 (i.e, zero).

What are the disadvantages of two’s complement arithmetic?

Two’s complement arithmetic works for addition and subtraction. However, multiplying and dividing two’s complement values requires different algorithms for signed and unsigned operations. In turn, this means that the ALU requires different hardware for signed and unsigned operations. Because the ordering of signed and unsigned numbers is different, you have to provide different comparison and branch operations for signed and unsigned values. This is not hard to do in hardware, but it is a potential source of programmer error.

What range of values can be represented by unsigned integers? Give examples using 8-bit and 16-bit integers.

An m-bit unsigned integer can represent the values 0 to 2m – 1.

An m-bit signed integer can represent the values  –2m-1 to 2m-1 – 1.

In 8 bits the range is 0 to 255 (unsigned) and -128 to + 127 (signed)

In 16 bits the range is 0 to 65,535 (unsigned) and -32,768 to + 32,767 (signed)

How is a two’s complement number calculated?

The negative representation of a number N in m bits is defined as 2m – N. In practice, the computer does not have to perform this calculation because inverting all the bits of N and adding 1 yields the same result.

In 8-bit arithmetic, what is the binary representation of -42?

The integer 42 is represented by 00101010.

The corresponding two’s complement is 11010101 + 1 = 11010110.

What is arithmetic overflow?

Because two’s complement arithmetic is valid only for numbers in the range –2m-1 to 2m-1 – 1, any operation that takes the result out of this range will be incorrect. Such an error is called arithmetic overflow.

When does arithmetic overflow occur during addition and subtraction?

If two positive values are added and the result is greater than 2m-1 – 1, or if two negative numbers are added and the result is less than –2m-1. Note that arithmetic overflow is indicated by the sign-bit of the result being different to the sign bit of the two numbers being added.

How is a two’s complement value expanded from m bits to n bits where n > m?

The sign-bit is simply replicated to fill the new bit positions. Consider the conversions of 42 and -42 in 8 bits to 16 bits.

42 = 00101010 in 8 bits and becomes 0000000000101010 in 16 bits

-42 = 11010110 in 8 bits and becomes 1111111111010110 in 16 bits.

Example

Suppose you are using four digit ten’s complement arithmetic. Consider the following operation.

 0073

+PQRS

X0048

What are the values of P, Q, R, and S. Does the value of X matter?