Home Up

Home Teaching Glossary ARM Processors Supplements Prof issues About

Error Detecting Codes

This is an introductory article on the way in which errors occur in digital systems and how they are detected.

The reason we use digital systems is two-fold. First, it’s very easy to manufacture digital integrated circuits using semiconductor technology, and, second, digital systems are more robust and error tolerant than analog systems. Analog signals are prone to errors due to noise and circuit imperfections. A digital signal can always be reconstructed unless it suffers such severe distortion that the voltage representing a 1 level is changed sufficiently to make it a 0 level (or vice versa).

Digital errors never occur in purely digital circuits. However, memory devices like DRAM store data in an analog form as a charge on a capacitor and that charge can be affected by events such as the passage of an ionizing particle through a memory cell. It has been reported that such errors are of the order of once per month in a 128 MB device. Flash memory is also subject to errors because the internal storage mechanism can be damaged by repeated write and erase cycles. When digital data is transmitted from point-to-point, data can be corrupted by errors induced from other circuits (in effect, the circuit connections act as antennas and pick up signals). Finally, any data that is transmitted over long distanced via wireless links is subject to errors caused by interference and noise. The most extreme case is in data transmitted from satellites and spacecraft where the received single is actually far weaker than background noise.

Clearly, errors are not a good thing. An error in a program can cause a crash or incorrect operation of the program. An error in data can be pretty meaningless (a bit dropped in a movie), inconsequential (a “the” in a block of text being changed into “thg”, or catastrophic (an error in a spacecraft navigation system).

There are two steps in dealing with errors. The first is error detection. Clearly, you can’t do anything until you realize that you have erroneous data. The second is error correction or recovery. Once you have found an error, you can either request a new copy of the data, or you can correct it by means of an error-correcting code.

Computers (i.e., digital systems) detect errors exactly like we do; for example, if you encounter the word qmick in English text, you know it is incorrect because there is no qmick in the English language. In other words, we have to encode data in such a way that any change from the correct value is obvious.

An n-bit binary value has 2n possible combinations, from 000…0 to 111...1. You can’t detect an error in such a word because all combinations are valid. You have to reduce the number of possible values to a smaller subset. Let’s begin with an example, the parity bit.

Parity

The simplest way of detecting a single error is called a parity bit. This is essentially the exclusive OR of all the bits of the word. Consider a word with four bits in total, P,C,B,A. We reserve one bit as the parity P, and the other three bits are C,B,A. If we define parity P as CÅBÅA, we can write all the legal combinations as:

P C B A

0 0 0 0

1 0 0 1

1 0 1 0

0 0 1 1

1 1 0 0

0 1 0 1

0 1 1 0

1 1 1 1

The parity bit is called an even parity because it ensures that the total number of 1s in the codeword is even. For the purpose of parity generation,  number zero is defined as even.

Note how we have only eight legal combinations out of 16 possible combinations of four bits, because one bit is no longer a variable; it’s a function of the other three bits. We have taken a 3-bit sourceword, C,B,A, and converted it into a 4-bit codeword, P,C,B,A.

Suppose the original souceword is 010. The parity bit is 0Å1Å0 = 1 and the codeword is therefore 1010.

If we change a single bit of this codeword, we get 0010 or 1110 or 1000 or 1011. In each case the parity of the codeword is odd and the word is invalid (i.e., it does not correspond to a legal codeword). In other words, we can detect a single bit error.

If we get two errors in a codeword, the parity is preserved; for example, if the codeword is 1010 and the leftmost two bits are changed, the result is 0110  which is a valid codeword because the parity is even. Consequently, an error-detecting code can detect some errors but not ALL errors. A single-bit parity code can detect an odd number of errors but not an even number of errors. This is equally true of English – if this has one error and becomes thes we can detect it, but if there are two errors and it becomes them we can’t detect an error because them is a valid English word.

Where should the parity bit go in a word? It doesn’t matter. Each bit in a codeword has the same chance of corruption. By convention, the parity bit is often the most-significant bit of the code word.

The parity bit can be even (i.e., the total number of 1s in the word is even) or it can be odd (the total number of 1s is odd). In principle, doesn’t matter whether you use an even or an odd parity bit. However, if the sourceword is all zeros, the parity bit will be zero and the codeword will be all zeros. Some engineers don’t like an all-zeros word, because you can’t tell the difference between a word that is 000…00 and a system failure that returns 000…00.

The Hamming Distance

An important concept associated with error detecting codes is the Hamming distance between two binary words of the same length. The Hamming distance is a measure of how different the two words are.

Let’s look at a 3-bit codeword with even parity. Assume that the set of codewords {000, 011,110,1010} with even parity are legal. If we represent all eight possible codwords as the corners of a cube (see figure 1), it becomes clear that each valid codeword differs from an illegal codeword by one bit, and from another legal codeword by two bits. This is the key to error detection; a single error always changes a valid code  from a legal codeword  to an illegal codeword. Consequently, each legal codeword must differ from any other legal codeword by at least two bits.

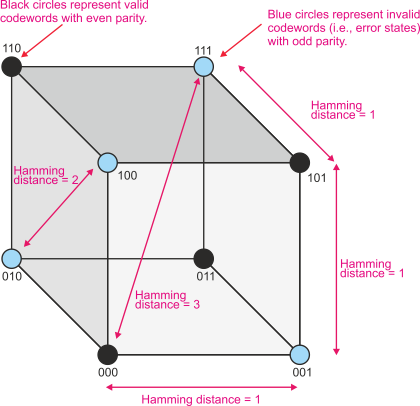
Figure 1 All possible combinations of a 3-bit code with even parity

If you have two n-bit words X and Y, the Hamming distance between X and Y is the number of positions in which the bits of X and Y differ. The minimum Hamming distance is 0 (i.e., X and Y are the same) and the maximum Hamming distance is m (i.e., X is the complement of Y). Consider:

X = 00001111

Y = 11111111 Hamming distance  = 4

X = 10101011

Y = 10110011 Hamming distance = 2

Redundant Bits

Any error detecting code of n bits takes an m-bit sourceword and generates an r redundant bits to generate an m-bit codeword, where n = m + r. In a single-bit parity code, the value of r = 1 and m = n – 1. Figure 2 illustrates the relationship between sourceword and codeword. The nature of the actual code determine the value of r. A  high probability of error may requires many redundant bits to provide adequate error detecting capability.

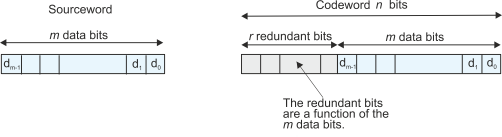
Figure 2 Data and redundant bits

Assume we transmit n-bit messages, where m bits are data bits and r = n - m bits are redundant check bits. Imagine an n-dimensional space in which each point is represented by the value of an n-bit signal. This n-dimensional space contains 2n possible elements (i.e., all the possible combinations of n bits). However, an m-bit source code can provide only 2m unique messages; that is,  2m binary combinations are valid out of the 2n possible codewords. Should a code word be received that is not one of these 2m legal values, an error is assumed. We can generalize the 3D code space of figure 1 into the n-dimensional code space of figure 3.

If r check bits are added to the m message digits to create an n-bit code word, there are 2n = 2m + r possible code words. The n-dimensional space will contain 2m valid codewords, 2n possible codewords and 2n - 2m  = 2m(2n-m - 1) =2m(2r - 1) error states.

If we read a word from memory or from a communication system, we can check its location within the n-dimensional space. If the word is located at one of the 2m valid points we assume that it's error free. If it falls in one of the 2n - 2m error states, we can reject it.

Errors

The theory of errors in digital systems marks the beginning of modern digital data transmission systems, information theory and coding. The father of information theory is Claude E. Shannon ad his pioneering work appears in the Bell System Technical Journal in 1948. However, Harry Nyquist also made a major contribution in 1924 when he discussed the rate at which data could be transmitted over a telegraph line.

Much of information theory uses the notion of the symmetric binary channel where the probability of a 0 changing to a 1 and a 1 changing to a 0 (due to noise) is equal. In a real system this may not be the case because the actual probability depends on the nature of the noise and the switching threshold of digital circuits. Similarly, random noise is often assumed to have a Gaussian distribution (that is, the amplitude of the nose has a Gaussian bell curve distribution). In practice, noise is often bursty; that is, errors occur in bursts. Error bursts occur because of the electromagnetic pulse generated by a lightning strike or an elevator motor starting.

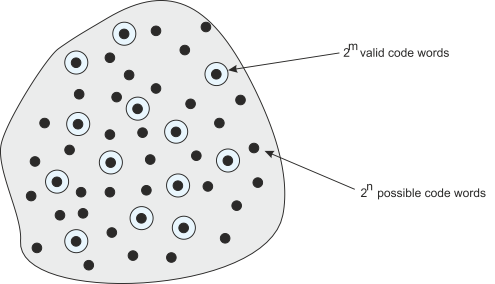
Figure 3 Code space

In the next section we look at an extension of error detecting codes, EDCs. These codes are error correcting codes, ECCs. Note that we should really write error detecting and correcting codes, but the term error correcting codes has become common.