Home Up

Home Teaching Glossary ARM Processors Supplements Prof issues About

Error-correcting codes

An error detecting code determines whether a given codeword is valid or contains one or more errors. Of course, this statement is not entirely correct because some errors can convert one valid codeword into a different valid codeword. In practice, an error detecting code is chosen to ensure that the probability of missing an error is acceptably low.

An error correcting code, ECC, takes error detection one step further. An error in a codeword can be detected and corrected. However, it is still possible to both miss errors and to make erroneous corrections (i.e., a codeword with an error can be corrected to the wrong sourceword).

Redundant bits are used to enable error detection. Even more redundant bits are required for error correction. Consider the simplest scheme, bit triplication. Bit triplication does what you’d expect. Each source bit is triplicated so that the sourceword 00101 would become the codeword 000000111000111. Triplication is not a practical form of error correcting code because it triplicates the number of data bits.

If a single error occurs in a three-bit group, the error can be corrected’ for example, a 1 is stored/transmitted as 111 and the three invalid codewords 011, 010, and 110 can be corrected the source bit 1. Note that two errors in a group detect and error but lead to a wrong correction. If the group 111 becomes 010, it is falsely corrected to 0.

A triplicated-bit code can be made more effective by interleaving bits. Suppose bit a is transformed to bits a0,a1,a2, and so on. The 3-bit sourcecode abc becomes a0,a1,a2, b0,b1,b2, c0,c1,c2. We can interleave this to get:

a0,b0,c0, a1,b1,c1, a2,b2,c2

Using the sourecode 010 we get 010010010. If bits 6 and 7 are corrupted the new codeword is 001010010. If we de-interleave the code, we get 000 011 100. This can be corrected to 0 1 0. Interleaving helps deal with bursty errors where errors tend to occur within goups of bits.

What do we need to detect and correct one or more errors?

Figure 1 illustrates six codes with Hamming distances 1 to 6. Remember that a Hamming distance of i means that there are i bits differently between any two valid codewords. It is not possible to have two valid codeswords where there are less than i bits that differ.

In the first case where the Hamming distance is 1, all possible codewords are valid and each codewords is 1 (or more) Hamming lengths from its neighbor. Ann error can neither be detected nor corrected.

In the second case, the Hamming distance is 2 (e.g., the parity bit code). A single error moves a valid codeword to an invalid state and a single error can be detected.

In the third case, the Hamming distance is 3.  In this case three errors are needed to change one valid codeword into another valid codeword. Consequently this code is able to detect two errors. However, if a single error occurs, the invalid codeword will be closed to one valid codeword than any other. Now, it becomes possible to correct an error by selecting the valid codeword closest to an invalid error state. Note that two errors would lead to the situation in which an error is detected and the wrong correction mode.

When the Hamming distance is 4 we have a situation in which up to three errors can be detected. One error can be corrected. Two errors least to a state midway between two valid codewords so that all you can stay is that two errors have occurred.

With a Hamming distance of 5 we can detect up to four errors and correct two errors.

Finally, a Hamming distance of six allows us to detect up to five errors and to correct two errors.

The Hamming distance tells what number of errors can be detected and corrected. The major problem is design codes in which all codewards are separated by a minimum Hamming distance. This topic is beyond the scope of this article. However, we will look at the simplest class of error correcting code..

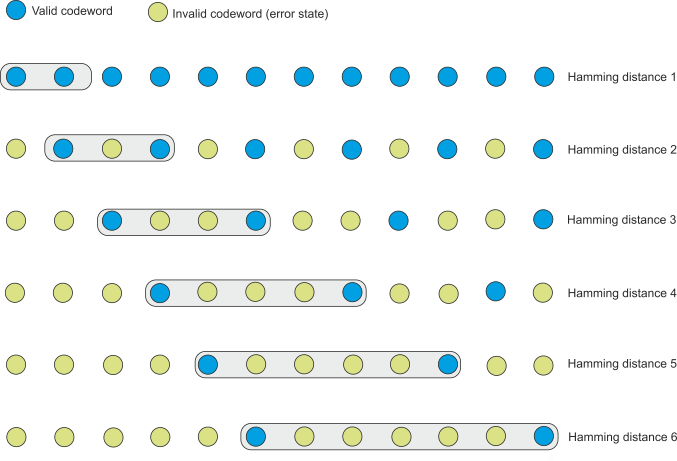
Figure 1 Codes with Hamming distances from 1 to 6

Hamming Codes

Hamming codes  take an m-bit sourceword and generate r parity check bits to create an n-bit codeword. The r parity check bits are selected so that a single error in the codeword can be detected, located and therefore corrected.

Hamming codes are designated Hn,m where, for example, H7,4 represents a Hamming code with a code word of 7 bits and a source word of 4 bits. We are going to demonstrate the simplest practical Hamming code. The following sequence of bits represents a H7,4 code word:

Bit position 7 6 5 4 3 2 1

Code bit  I4 I3 I2 C3 I1 C2 C1

Ii = source bit i, Ci = check bit i.

The information (i.e., source word) bits are numbered I1, I2, I3 and I4, and the check bits are numbered C1, C2, and C3. Similarly, the bit positions in the code word are numbered from one to seven. The check bits are located in binary positions 2i in the code word (i.e., positions 1, 2, and 4). Note how the check bits are interleaved with the source code bits.

The three check bits are generated from the source word according to the following parity equations.

C3  = I2  Å I3  Å I4

C2  = I1  Å I3  Å I4

C1  = I1  Å I2  Å I4

For example, C3 is the parity bit generated by information bits I2, I3, and I4, etc. Suppose we have a source word equal to I4,I3,I2,I1 = 1,1,0,1. The check bits are calculated as

C3 = 0 Å 1 Å 1 = 0

C2 = 1 Å 1 Å 1 = 1

C1 = 1 Å 0 Å 1 = 0

The code word is therefore:

I4,I3,I2,C3,I1,C2,C1= 1,1,0,0,1,1,0

Suppose now that the code word is corrupted during storage (or transmission). Assume that the value of I3 is switched from 1 to 0. The resulting code word is now: 1000110. Using the new code word we can recalculate the check bits to give:

C3  = 0 Å 0 Å 1 = 1

C2  = 1 Å 0 Å 1 = 0

C1  = 1 Å 0 Å 1 = 0

The new check bits are 1,0,0 and the stored check bits are 0,1,0. If we take the exclusive OR of the old and new check bits we get 1 Å 0, 0 Å 1, 0 Å 0 = 1,1,0. The binary value 110 expressed in decimal form is 6 and points to bit position 6 in the code word. It is this bit that is in error. How does a Hamming code perform this apparent magic trick? The answer can be found in the equations for the parity check bits. The check bits are calculated in such a way that any single bit error will change the particular combination of check bits that points to its location.

The Hamming code described above can detect and correct a single error. By adding a further check bit we can create a Hamming code that can detect two errors and correct one error.