Home Up

Home Teaching Glossary ARM Processors Supplements Prof issues About

Introduction to Gates and Digital Circuits

These notes cover part of the body of knowledge required by the BCS Certificate Exam. Here, we explain what gates are, how they are used, and how simple digital circuits are constructed.

Boolean algebra is the algebra of logic and can be used to design digital systems. Digital systems are constructed from real components such as memory chips and microprocessors. However, all digital circuits such as memory components can be constructed from primitive devices called gates.

Every digital circuit (apart from peripherals and communication systems) can be constructed from nothing other than a large collection of gates. A system as complex as a computer may require billions of gates.

In this article we a look at simple digital circuits that contain only a handful of gates. Here we discuss only combinatorial circuits. A combinatorial circuit has inputs and one or more outputs. The output is a function only of its inputs. If the output is y and the inputs are x0,x1,x2,…xi, then y = f(x0,x1,x2,…xi) where f is some function (i.e., the behaviour of the circuit).

There are other circuits called sequential circuits whose output is a function of both the inputs and the circuit’s previous state. These circuits exhibit memory because the output depends on what has happened prior to the current inputs. The most obvious example of a sequential circuit is the counter. The next count depends on the previous count. We do not discuss sequential circuits in this article.

Gates

There are three classes of gate: fundamental, derived, and the basic circuit. We look at each of these groups in turn.

Fundamental Gates

There are three basic gates that are derived from the fundamental postulates of Boolean algebra. The AND gate, the OR gate and the NOT gate. All Boolean functions can be implemented with these gates.

Derived Gates

There are two derived gates that can be constructed from an AND gate plus a NOT gate, or an OR gate plus a NOT gate; they are called NAND and NOR gates respectively. The terms NAND and NOR are contractions of Not AND, and Not OR, respectively. The reason that special names were given to these gates is because they both have one very important property. Every digital circuit can be constructed with NAND gates alone; and every digital circuit can be constructed with NOR gates alone.

Another derived gate is the XOR (exclusive OR) gate that can be constructed from two AND gates, two NOT gates, and an OR gate. The XOR gate is of interest because of its mathematical and logical properties and because it is used so frequently in digital circuits.

Basic Circuits

There are an infinite number of circuits that you can construct with gates. Some circuits are so frequently used that they are given names such as the decoder, multiplexer, and adder. Here we will look as some basic circuits (i.e., basic building blocks).

Gate Packages

Gates are available (i.e., manufactured and packaged) in various forms. Consider:

SSI (Small Scale Integration) The very first integrated circuits were called small scale integration and typically included a handful of gates on a single chip; for example, four NAND gates.

MSI (Medium Scale Integration) Medium scale integration chips have sufficient gates to create a basic building block such as an adder or a multiplexer. In general, you would use SSI and MSI circuits to build either a relatively simple digital system (e.g., a burglar alarm or fire alarm) or to connect together more complex systems (e.g., connect a microprocessor to an interface).

LSI and VLSI LSI (large scale integration) and VLSI (very large scale integration) refers to circuits of the complexity of microprocessors. In this article, we are going to look only at SSI circuits.

Fundamental Gates

The AND gate

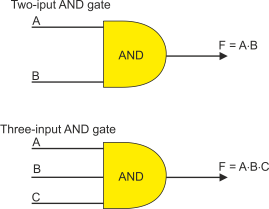
An AND gate is a circuit with two or more inputs and a single output. It is called an AND gate because the output is true, if and only if, all its inputs are true. That is, if the inputs are A, B, C, the output F is true if A is true and B is true and C is true; that is F = A×B×C.

The simplest AND gate has two inputs; for example F = A AND B = A×B.

By convention a truth table, is often used to illustrate the behaviour of a gate (or circuit). A truth table defines the output for each possible state of the input; for example, a gate with one input has two possible states (0 and 1). A gate with two inputs has four possible states (00, 01,10,11). A gate with three inputs has eight possible states (000, 001, 010, 001, 100, 101, 110, 111). A gate with n inputs has 2n possible states. In general, truth tables are not normally used with systems having more than five inputs because they rapidly grow complex and unwieldy as the number of inputs increases.

Tables 1 and 2 give the truth tables for a 2-input and a 3-input AND gate. Note that some order the input variables A,B,C,D and others use D,C,B,A. There is no absolute rule. I generally (but not always) prefer the sequence D,C,B,A. Why? Because when the input variables represent binary integers the binary value 1000 represents decimal 8 and the most significant bit is on the left. If we give these bits names, it is more natural to represent the most significant bit by D rather than A because if we later extend the system to 5 bits, the new most significant bit will be E. If we represent the most significant bit by A, we would have to reliable all bits when moving from 4 to 5 bits. This naming problem arises because we write from left to write because of the Latin alphabet but number from right to left because we use Arabic numbers.

Table 1 The truth table for a 2-input AND gate

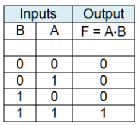
Table 2 The truth table for a 3-input AND gate

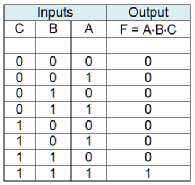
Figure 3 shows the circuit representation of a 2-input AND and a 3-input AND gate. Note that the shape of the gate defines its function.

Figure 3 Circuit symbols for 2-input and 3-input AND gates

One way of looking at the AND gate is to say that it detects an all 1s condition by outputting a 1 when all inputs are 1. Another way of looking at an AND gate is to say that it detects any 0 at an input by outputting a 0 if any input (or more than one input) is 0.

The OR Gate

An OR gate is a circuit with two or more inputs and a single output. It is called an OR gate because the output is true, if any of its inputs are true. That is, if the inputs are A, B, C, the output F is true if A is true or B is true or C is true; that is F = A + B + C. Note that the Boolean OR is not the same as the English language or! Where you say, “Do you want tea or coffee”, you mean one or the other (i.e., the exclusive or). The Boolean OR of three inputs is true for states 001, 010, 100, 110, 011, and 111.

The simplest OR gate has two inputs; for example F = A OR B  = A + B.

Table 3 give the truth tables for a 2-input and a 3-input OR gate.

Table 3 The truth table for a 2-input OR gate and a 3-input OR gate

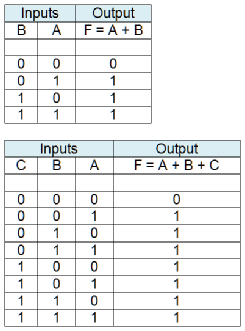
Figure 4 gives the circuit representation of a 2-input OR and a 3-input OR gate. Like the AND gate, the shape of the gate defines its function.

Figure 4 Circuit symbols for 2-input and 3-input OR gates

One way of looking at the OR gate is to say that it detects an “any 1s condition” by outputting a 1 when one or more of the inputs are 1. Another way of looking at an OR gate is to say that it detects an “all 0s condition” at its inputs by outputting a 0.

The NOT Gate

The NOT gate which is also called an invertor or complementer is the simplest gate: its output is a complement of the input. The truth table for a NOT gate is given below. A NOT gate can have only one input.

Table 4 The truth table for a NOT gate (invertor or complementer)

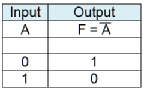
Figure 5 illustrates the NOT gate. Note that the inversion function is indicated by the little circle at the output. In fact, you can put such a circle at the input or output of any gate to indicate inversion.

Figure 5 Circuit symbol for a NOT gate

Simple Circuits

Before we look at derived gates, we are going to demonstrate some simple circuits. The first circuit in figure 6 uses four gates: three AND gates and OR gate. It has three inputs A, B, C and a single output F.

How do we interpret this circuit? How do we analyse it? What conventions are used when drawing a circuit?

Figure 6 A circuit with four gates

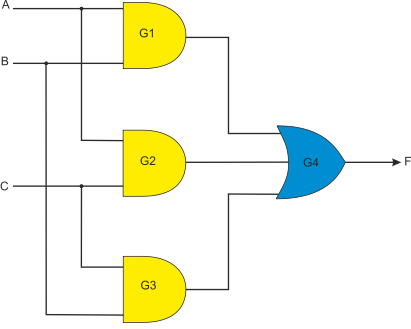
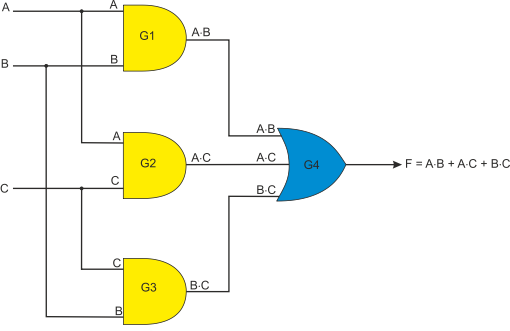
Figure 7 shows the same circuit with some values marked. Let’s begin with the conventions.

The most important aspect of a circuit diagram is its topology; that is, the circuit is all about the connections or paths between circuit elements, and not about how they are laid out or presented. If you were to draw a circuit diagram on a sheet of rubber and then pull, twist and stretch it, it would still have the same topology (and function) even if it looked entirely different.

Figure 7 A labelling signals in the circuit of figure 6

Having pointed this out, there are some practical conventions concerning circuit diagrams. First, signals generally flow from left to right with inputs at the left hand side of the figure; this is done because we write left to right when using the Roman alphabet.

Second, if two circuit paths simply cross, they are not connected. If two paths are connected, a dot is normally placed at their intersection.

Third, the signal level at each point along a path (i.e., wire or printed circuit track) is the same everywhere along that path; a corollary of this is that the same path cannot be driven into two different logical states at the same time.

Figure 7 demonstrates that AND gate G1 receives signals A and B and generates an output A×B. Similarly, gate G2 receives A and C and generates A×C, and gate G3 receives B and C and generates B×C.

OR gate G4 receives inputs A×B, A×C, and B×C, and generates the output F = A×B + A×C + B×C. Incidentally, this expression is in its simplest from and cannot be simplified.

What does this circuit do? Some students may be able to look at the equation and figure out what this represents. However, a more methodical approach is to use a truth table. We’ve got three inputs which means we require a truth table with 8 rows. Consider the table 5.

Table 5 The truth table for the circuit of figure 7

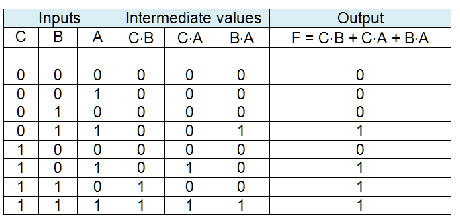
We have tabulated all 8 possible inputs and have provided columns for intermediate values (A×B, A×C, and B×C) together with an output column. Including intermediate values makes it very easy to construct the truth table because we just have to OR them to get the final output F.

So, what does this circuit do? Note that the output is symmetric; there are four 0s and four 1s. The output is 0 of two or three of the inputs are 0, and the output is 1 if two or three of the inputs are 1. In other words, the circuit detects whether the majority of inputs are 0 or 1. It’s a voting circuit, returning a value that corresponds to the larger numbers of 1s or 0s in the input.

Example – Creating a Circuit from an Expression

Now let’s consider another example, where we are given a Boolean expression and have to create a circuit. Suppose the expression is F = (A×B)×C + A’×B’×C’ and we have to implement this exactly as in the equation with no rearranging or simplification.

Clearly, the output F is generated from the sum of two product terms; that is, (A×B)×C and A’×B’×C’. We can draw the output of the circuit required to perform this operation (Figure 8).

Figure 8 Creating a circuit from a Boolean expression – step 1

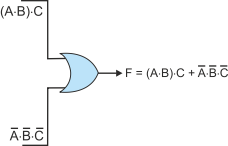
This now leaves us with the two terms (A×B)×C and  A’×B’×C’ to generate. These are both product terms. The first can be generated by a 2-input AND gate with inputs (A×B) and C, and the second with a 3-input AND gate with inputs A’, B’, and C.

Figure 9 Creating a circuit from a Boolean expression – step 2

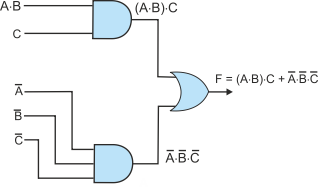
We still have to generate the product term A×B and the negated terms A’, B’, C’. The final circuit diagram, figure 10, demonstrates this last step.

Figure 10 Creating a circuit from a Boolean expression – step 3

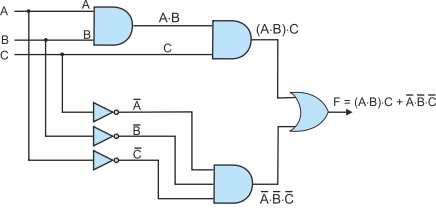
Derived Gates

The two most important derives gates are the NAND and NOR gates which are an AND gate followed by an invertor, and an OR gate followed by an invertor, respectively.

The truth tables for 3-input NAND and NOR gate are given in Table 6. There is nothing mysterious about these gates. As the truth tables show, they are the same as the respective AND and OR truth tables but with the output complemented. However, these gates are important for two reasons. The first is that they can be implemented more efficiently in silicon than the corresponding AND and OR gates. The second, is that you can construct an OR gate from a NAND gate and an AND gate from a NOR gate. Moreover, you can construct an invertor from either a NAND gate or a NOR gate. Consequently, all digital circuits can be constructed from NAND (or NOR) gates only.

NAND and NOR Gates

Table 6 The truth table for a 3-input NAND gate

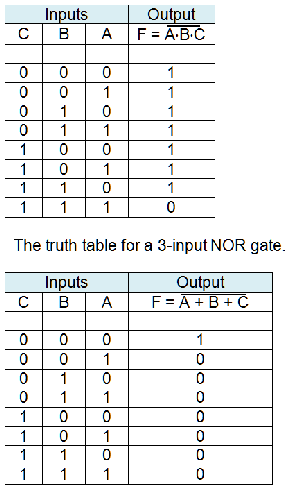
Figure 11 shows the circuit symbols for NAND and NOR gates. The shapes of these symbols are the same as the corresponding AND and OR gates. The only difference lies in the bobble at the output that indicates the inversion operation.

If both inputs of a 2-input NAND gate (all all three inputs of a 3-input NAND gates) are wired together, all inputs are 0 or 1. The output is then 1 or 0, respectively. Consequently a NAND gate can be used as a NOT gate (inverter). The same is true for the NOR gate.

Figure 11 Circuit symbols for NAND and NOR gates

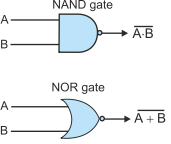
Example of a NAND circuit

Let’s look at a circuit constructed from NAND gates only, figure 12. This is a classic example because it is found in most textbook and demonstrates how an EOR function (which we will explain later) can be constructed from four NAND gates.

Figure 12 Circuit  using four NAND gates

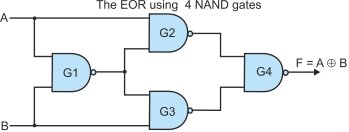
Let’s analyse this circuit. To do this we will introduce intermediate values. Figure 13 includes the addition of intermediate points and an analysis of the signals flowing through the circuit. At each stage (going from left to right) we have presented the output of a gate and then simplified it where possible.

We are left with a final output of F = A×B’ + A×B’. This is the exclusive OR function. It’s called that because it’s rather like the English use of or. The output is true if A alone is true or if B alone is true, but not if both A and B are true. It’s a one or the other circuit. The exclusive or function, XOR, is one of the most important functions in digital systems because it is at the heart of all arithmetic circuits and almost all data encoding and decoding circuits.

Figure 13 Analyzing the circuit using four NAND gates

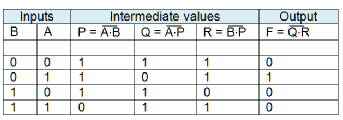
We can also analyse the circuit with a truth table by plotting intermediate values, table 7. This is perhaps easier than the analytic approach in this case. Here the output is F = A×B’ + A’×B which is exactly the same as we derived analytically.

Table 7 Analysing the circuit of figure 13

The Exclusive OR

We have already introduced the exclusive OR (or EOR, XOR – both abbreviations are commonly used). Figure 14 provides the circuit symbol for an exclusive OR and Table 8 gives its truth table. Most texts describe the exclusive OR as a gate with two inputs (unlike the AND and OR gates that can have any number of inputs). However, it is possible to extend the exclusive OR to a circuit with n inputs whose output is 1 if the number of 1s in the input is odd, and whose output is 0 if the number of 1s in the input is 0 or even (such a circuit is called an even parity detector). Here, we discuss only the 2-input exclusive OR.

Figure 14 The Symbol for the Exclusive OR

Table 8 Exclusive OR truth table

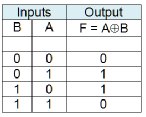
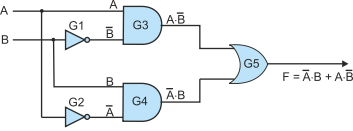
From the truth table we can write F = A×B’ + A’×B. Figure 15 shows how the EOR gate can be constructed using AND, OR and NOT gates.

Figure 15 The EOR Gate constructed from AND, OR and NOT gates

The EOR function performs several functions:

 It’s output is 1 if both inputs are different (i.e., 0,1 or 1,0)

 It can be used to compare binary values

 It calculates the modulo 2 sum of two bits (in modulo 2 arithmetic there is no carry)

 Two EOR gates can be used to create a full adder that adds three bits (additional logic is required).

Simple Digital Circuits

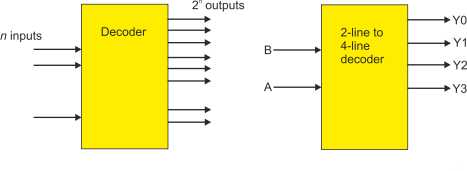
The Decoder

A decoder takes an n-bit input and uses it to generate one-of-n outputs. For any binary code at the inputs, one and only one of the outputs is set to 1. All other outputs are 0. Figure 16 describes a decoder. On the left is a generic n-line to one-of-2n-lines decoder. On the right is a simple 2-line to 4-line decoder.

Figure 16 The decoder

Consider the truth table for the 2-line to 4-line decoder, table 9. Here there are two inputs, A and B, and four outputs Y0, Y1, Y1, and Y3. Although many classroom problems define a problem with n inputs and one output, there is no reason why a digital circuit cannot have any number of outputs. When you have more than one output, you have to create a separate function for each output; that is, you treat the problem as having four separate truth tables, one for each output.

Table 9 Truth table for the 2-line to 4-line decoder

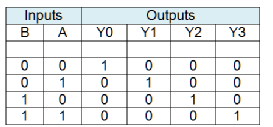
As you can see from table 9, each output is true for one unique value of the input. By inspection, we can write

Y0 = B’×A’

Y1 = B’×A

Y2 = B×A’

Y3 = B×A

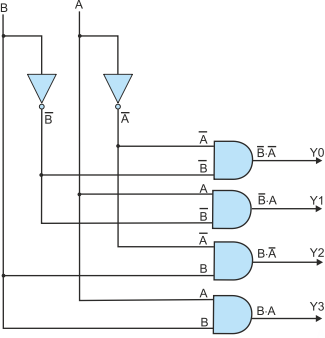
Figure 17 demonstrates how we might implement the decoder. Note that although there are four inversions in the equation, we need only two actual inverters as the figure demonstrates. Once we have inverted A to get A’ we can use it repeatedly in the same circuit.

Figure 17 Implementing the 2-line to 4-line decoder

Example of the Use of a Decoder

Here is a simple example of the use of a decoder. It demonstrates how a decoder can be used to select one of several actions. In this case, we are going to design a programmable logic element that can perform an AND, OR, NAND and NOR operation depending on the status of a 2-bit control input. Although this is a very simple example, it goes to the heart of computer design because a computer uses the bits of an op-code (instruction) to select between one of several operations.

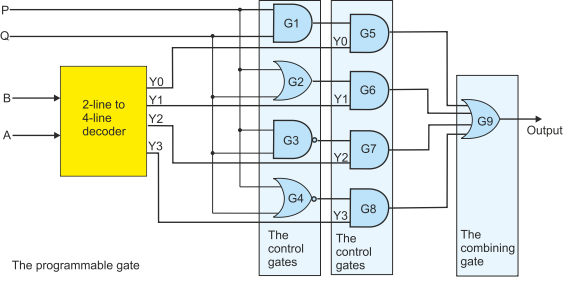
You can consider the circuits as using four vertical slices of gates to process the signals flowing left to right. At the left we have the 2-line to 4-line decoder. This decodes a 2-bit signal B,A into one of four values Y0 = 0,0, Y1 = 0,1, Y2 = 1,0, and Y3 = 1,1. Each of these signals selects a particular logic function.

The second slice, gates G1 to G4 each take in inputs P,Q to perform a logical function. G1 performs the AND, G2 performs the OR, G3 performs the NAND and G4 performs the NOR. So, at any instant we generate all four functions of P and Q.

The next line of gates G5, G6, G7, G8 are AND gates that perform a gating function (i.e., they pass or block a signal). If the control input (Y0 to Y3) is 0, the output of the corresponding gates is at 0 because X AND 0 = 0. If the control input is 1, then the input from the gate in the previous column is passed because X AND 1 = X.

Finally, all outputs from the control column are passed to G2, the combining gate. Since three of the signals from the control gates must be zero, the output of G9 will be the selected signal from the control gates.

Figure 18 Using a 2-line to 4-line decoder to implement programmable logic

This circuit has been designed to demonstrate the nature of gates and circuits. The circuit is correct, but we could build a far simpler version by using a truth table (see table 10). We will do that next.

In table 10, inputs B and A perform the programming (logic selection) and inputs P and Q are the logic inputs to be processed.

Table 10 Truth table for a programmable logic element

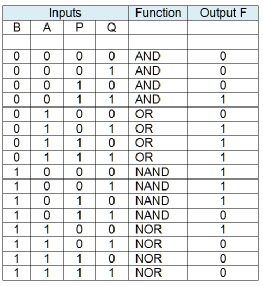
The output is

F = B’×A’×P×Q + B’×A×P’×Q + B’×A×P×Q’ + B’×A×P×Q + B×A’×P’×Q’ + B×A’×P’×Q + B×A’×P×Q’ + B×A×P’×Q’

We can simplify this:

F = B’×A’×P×Q + B’×A×Q’(P’ + P) + B’×A×P×Q + B×A’×P’(Q’ + Q) + B×A’×P×Q’ + B×A×P’×Q’

F = B’×A’×P×Q + B’×A×Q’ + B’×A×P×Q + B×A’×P’ + B×A’×P×Q’ + B×A×P’×Q’

F = (B’×A’ + B’×A)P×Q + A×Q’(B’ + B×P’) + B×A’(P’ + P×Q’)

F = B’×P×Q + A×Q’×B’ + A×Q’×P’ + B×A’×P’ + B×A’×Q’

This circuit could be implemented with four invertors, five 3-input AND gates, and one 5-input OR gate.

The Multiplexer

A multiplexer is a circuit with several inputs, a control input, and an output. The control input is used to select which input is connected to the output; in other words, the multiplexer is an electronically controlled switch or router. You can think of the multiplexer as the inverse of the decoder we have just described.

The simplest multiplexer is the 2-to-1 multiplexer described in Figure 19 where the state of control input X determines whether the output F is A or B. We can say that the function of the multiplexer is:

IF X == 0 THEN F = A

               ELSE F = B

In other words, the multiplexer is a logic circuit that can perform a conditional operation.  Ultimately, all computers that implement branch instructions use a circuit that can be considered to be a multiplexer.

Figure 19 The 2-to-1 multiplexer

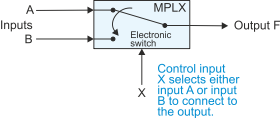
Table 11 gives the truth table for a 2-to-1 multiplexer. When X = 0, the output is A, and when X = 1, the output is B. We can write Boolean expression for F as F = X’×A + X×B. This expression can be implemented with an invertor, two AND gates and an OR gate. Figure 20 shows how the circuit can be implemented with four NAND gates (remember that an inverter can be constructed from a NAND gate with both its inputs connected together).

Table 11 The truth table for a 2-to-1 multiplexer

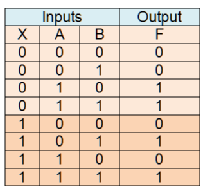
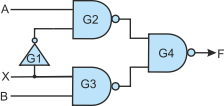
Figure 20 The 2-to-1 multiplexer constructed with NAND gates (G1 is a NAND gate with both inputs connected together)

This article is available as a PDF file.