Home Up Fun with bits 1 DoublePrecisionFloatingPoint Interesting circuit TwosComplement

Home Teaching Glossary ARM Processors Supplements Prof issues About

Example of the Use of a Karnaugh Map with Don’t Care Conditions

Design a circuit with four inputs D, C, B, A that are natural 8421-binary encoded with D the most-significant bit. The output F is true if the month represented by the input (0,0,0,0 = January, 1011 = December) is a vacation  month for me. I can have a vacation at Christmas, Easter, July, my birthday (September), or my wife’s birthday (May). Since Easter can occur in either March or April, we have to include both months.

Step 1: The truth table

We now construct a truth table. Note that binary input 1100 to 1111 (12 to 15) do not represent valid months and cannot occur. Although the output F should be 0 for these months since the output does not represent a vacation month, it does not matter whether we choose F as 0 or 1. So, we put x in the output column to represent don’t care and we can later choose x as 0 or 1 to simplify the logic.

D  C  B  A  Month   F

0  0  0  0  Jan     0

0  0  0  1  Feb     0

0  0  1  0  Mar     1

0  0  1  1  April   1

0  1  0  0  May     1

0  1  0  1  June    0

0  1  1  0  July    0

0  1  1  1  Aug     0

1  0  0  0  Sept    1

1  0  0  1  Oct     0

1  0  1  0  Nov     0

1  0  1  1  Dec     1

1  1  0  0          x

1  1  0  1          x

1  1  1  0          x

1  1  1  1          x

Step 2 The Karnaugh map

We put 1s in the squares where F = 1, an x in don’t care squares and leave the remaining squares (that contain a zero) empty.

Step 3 The simplified Karnaugh map

The next step is to simplify the Karnaugh map by creating the smallest number of the largest groups of 1s. All 1s must be included in at least one group. Any 1 can be in more than none group. We can treat an x as a 1 if we can use it to make a larger group.

This solution is not unique because we could have created other groupings of 1s (but none simpler than this).

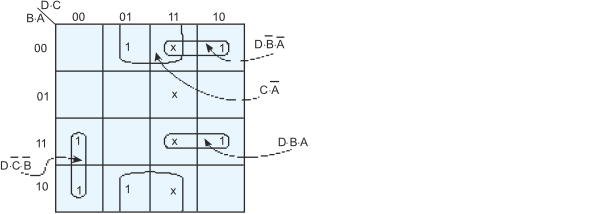
Step 4 Read the sum-of-product terms from the Karnaugh map

F = DB!A! + CA! + DBA! + DC!B!